我們看電影時，如果里面有汽車啟動時的鏡頭，會看到輪子顯示越轉越快，然后在某個時刻突然看起來變慢，甚至反轉。這是因為電影攝影機相當于一個固定的頻率Fs對連續的車輪采樣，當車輪轉速超過Fs/2并繼續提高時，看到的就是混疊干擾下的結果。

　　奈奎斯特采樣定理規定要使連續信號采樣后能夠不失真還原，采樣頻率必須大于信號最高頻率的兩倍(即奈奎斯特頻率)。當采樣頻率Fs低于奈奎斯特頻率時，重構的連續信號中原信號F/2以上的頻率會對稱的映象到了F/2以下的頻帶中，并且和F/2以下的原有頻率成分疊加起來。

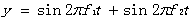
　　對我們以三種不同的頻率對這個函數進行采樣，分別得出欠采樣、臨界采樣、過采樣的頻譜，從三張頻譜中我們分析三種采樣與混疊的關系。

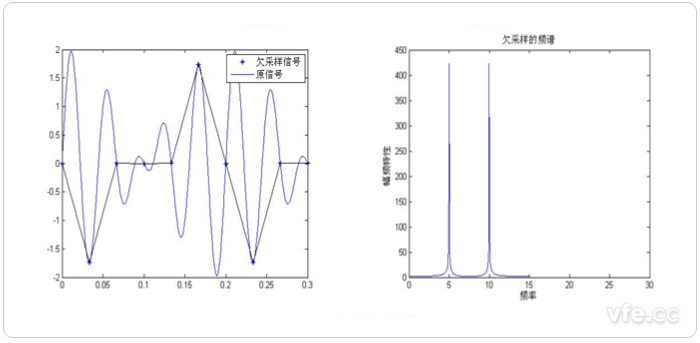
　　圖示1：欠采樣頻譜分析示意圖

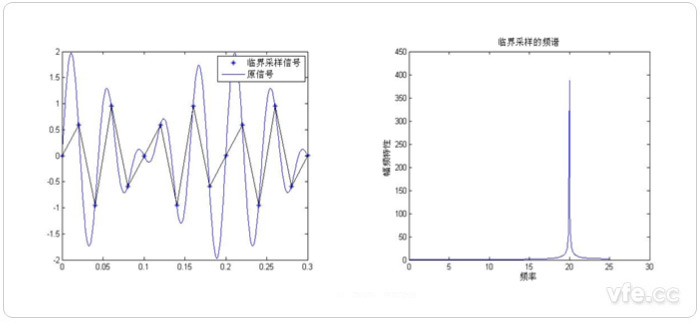
　　圖示2：臨界采樣頻譜分析示意圖

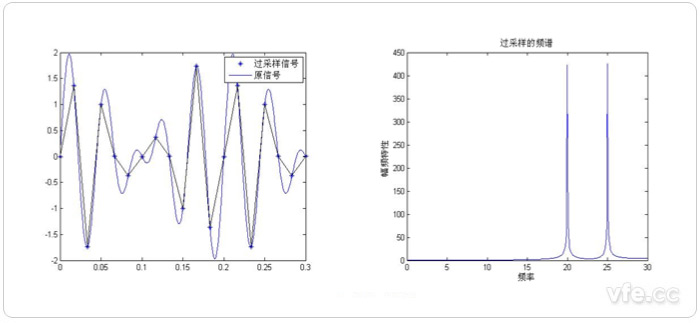
　　圖示3：過采樣頻譜分析示意圖

　　由圖示三種采樣頻率后的頻譜分析可知：欠采樣(FS<2F)會產生頻譜混疊；臨界采樣(FS=2F)也會產生混疊現象；過采樣(FS>2F)不會產生混疊現象。

　　混疊是數字信號處理中的一個重要概念，它是數字信號處理中的特有現象，是數字信號中離散采樣引起的。混疊現象會產生假頻率、假信號、會嚴重的影響測量結果，當采樣頻率小于模擬信號中所要分析的最高分量的頻率的2倍，就會發生。因此，我們通常采用以下兩種手段來消除混疊現象，保證測量精度。

　　1、 提高采樣頻率，使之達到被測信號最高頻率的兩倍以上；

　　2、 引入低通濾波器或提高低通濾波器的參數(該低通濾波器通常稱為抗混疊濾波器)，抗混疊濾波器可限制信號的帶寬，使之滿足采樣定理的條件。