一、采樣頻率定義

　　采樣頻率，也稱為采樣速度或者采樣率，定義了每秒從連續(xù)信號中提取并組成離散信號的采樣個數(shù)，它用赫茲（Hz）來表示。采樣頻率的倒數(shù)是采樣周期或者叫作采樣時間，它是采樣之間的時間間隔。通俗的講采樣頻率是指計算機每秒鐘采集多少個聲音樣本，是描述聲音文件的音質(zhì)、音調(diào)，衡量聲卡、聲音文件的質(zhì)量標(biāo)準(zhǔn)。

二、采樣定理

　　在進(jìn)行模擬/數(shù)字信號的轉(zhuǎn)換過程中，當(dāng)采樣頻率fs.max大于信號中最高頻率fmax的2倍(fs.max>=2fmax)，采樣之后的數(shù)字信號完整地保留了原始信號中的信息，一般實際應(yīng)用中保證采樣頻率為信號最高頻率的5～10倍；采樣定理又稱奈奎斯特定理。

　　采樣過程所應(yīng)遵循的規(guī)律，又稱取樣定理、抽樣定理。采樣定理說明采樣頻率與信號頻譜之間的關(guān)系，是連續(xù)信號離散化的基本依據(jù)。采樣定理是1928年由美國電信工程師H.奈奎斯特首先提出來的，因此稱為奈奎斯特采樣定理。1933年由蘇聯(lián)工程師科捷利尼科夫首次用公式嚴(yán)格地表述這一定理，因此在蘇聯(lián)文獻(xiàn)中稱為科捷利尼科夫采樣定理。1948年信息論的創(chuàng)始人C.E.香農(nóng)對這一定理加以明確地說明并正式作為定理引用，因此在許多文獻(xiàn)中又稱為香農(nóng)采樣定理。采樣定理有許多表述形式，但最基本的表述方式是時域采樣定理和頻域采樣定理。采樣定理在數(shù)字式遙測系統(tǒng)、時分制遙測系統(tǒng)、信息處理、數(shù)字通信和采樣控制理論等領(lǐng)域得到廣泛的應(yīng)用。

　　時域采樣定理：頻帶為F的連續(xù)信號 f(t)可用一系列離散的采樣值f(t1),f(t1±Δt)，f(t1±2Δt)，...來表示,只要這些采樣點的時間間隔Δt≤1/2F，便可根據(jù)各采樣值完全恢復(fù)原來的信號f(t)。

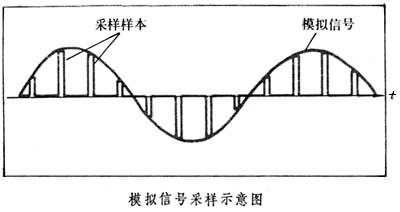
模擬信號采樣示意圖

　　時域采樣定理的另一種表述方式是：當(dāng)時間信號函數(shù)f(t)的最高頻率分量為fM時,f(t)的值可由一系列采樣間隔小于或等于1/2fM的采樣值來確定,即采樣點的重復(fù)頻率f≥2fM。圖為模擬信號和采樣樣本的示意圖。

時域采樣定理是采樣誤差理論、隨機變量采樣理論和多變量采樣理論的基礎(chǔ)。

　　頻域采樣定理：對于時間上受限制的連續(xù)信號f(t)（即當(dāng)│t│>T 時,f(t)=0,這里T =T2-T1是信號的持續(xù)時間），若其頻譜為F（ω）,則可在頻域上用一系列離散的采樣值來表示,只要這些采樣點的頻率間隔。

三、采樣基本過程

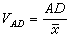　　測試時，采樣頻率的選擇將會影響到測試結(jié)果的好壞。采樣頻率高可以得到更有效的結(jié)果，但是，所采集的數(shù)據(jù)量也很大，浪費存儲空間，對CPU的要求也越高，從而使有效信號的存儲受到限制，或是增加了數(shù)據(jù)后處理的時間和復(fù)雜程度。如果采樣率太低，那么整個測試可能會沒有任何價值。

　　采樣的基本過程：信號產(chǎn)生后，進(jìn)行模數(shù)轉(zhuǎn)換，并捕捉離散信號

　　如下圖所示：　　

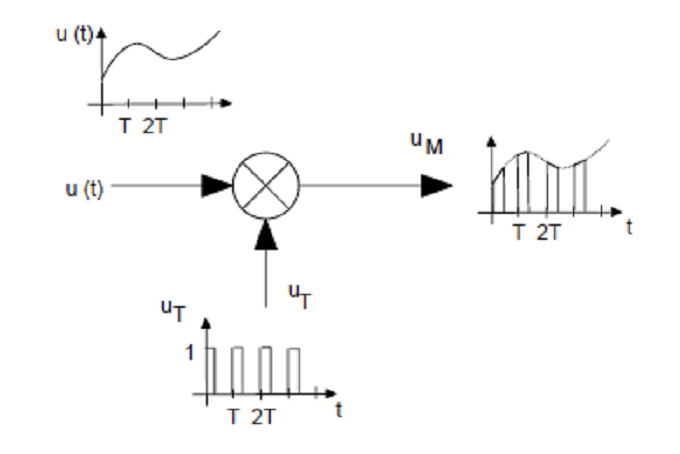
采樣過程

　　上圖簡單描述了采樣過程，它通常是由模數(shù)轉(zhuǎn)換器的采樣保持單元完成的。這個過程可以看作是被測量u(t)和周期采樣信號UT(t)相乘得到的結(jié)果。輸出的信號UM(t)仍然不是一個數(shù)字信號，因為它還需要經(jīng)過采樣保持單元（保持，然后被模數(shù)轉(zhuǎn)換器量化。顯然，當(dāng)采樣間隔變短時，輸出的信號將會更接近于輸入的原始信號。為了理解模擬輸入信號乘以采樣間隔T（>0）將會得到什么樣的結(jié)果，我們假想一個實驗：假如u（t）和uT(t)是兩個正弦信號，頻率分別為f和fT ，從公式sin(2πft) sin(2πfT t) = ?{cos[2π(f - fT )t] –cos[2π（f + fT )t]}，我們可以看到，相乘后得到了兩個復(fù)合頻率f-fT和f+fT。

---