
圖示:柵欄效應示意圖
柵欄效應描述的是信號采樣時只能得到采樣點的信息,而忽略了采樣間隔中數據信息的現象。不管是時域采樣還是頻域采樣,都有相應的柵欄效應,只是當時域采樣滿足采樣定理時,柵欄效應不會有什么影響。而頻域采樣的柵欄效應則影響很大,“擋住”或丟失的頻率成分有可能是重要的或具有特征的成分,使信號處理失去意義。減小柵欄效應可用提高采樣間隔也就是頻率分辨力的方法來解決。間隔小,頻率分辨力高,被“擋住”或丟失的頻率成分就會越少。但會增加采樣點數,使計算工作量增加。解決此項矛盾可以采用如下方法:在滿足采樣定理的前提下,采用頻率細化技術(ZOOM),亦可用把時域序列變換成頻譜序列的方法。
例如:505Hz正弦波信號的頻譜分析來說明柵欄效應所造成的頻譜計算誤差。
設定采樣頻率fs=5120Hz,軟件中默認的FFT計算點數為512,其離散頻率點如下式表達:
fi= i.fs/N =i.5120/512=10×i(i= 0,1,2,…,N/2)
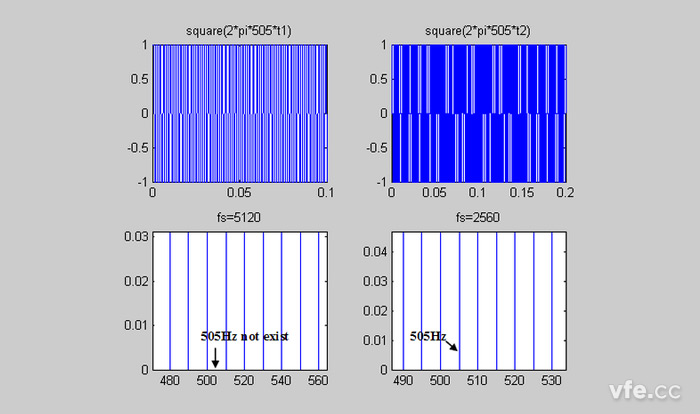
圖示:505Hz正弦波信號的頻譜分析示意圖
如上圖505Hz正弦波信號的頻譜分析示意圖所示,位于505Hz位置的真實譜峰被擋住看不見,看見的只是它們在相鄰頻率500Hz或510Hz處能量泄漏的值。若設fs=2560Hz,則頻率間隔df=5Hz,重復上述分析步驟。這時在505Hz位置有譜線,我們就能得到它們的精確值。從時域看,這個條件相當于對信號進行整周期采樣,實際中常用此方法來提高周期信號的頻譜分析精度。因此,在對周期信號傅里葉處理時,解決柵欄效應以致解決泄露效應的一個極為有效的措施是所謂“整周期截取”;而對于非周期信號,如果希望減小柵欄效應的影響,盡可能多地觀察到譜線,則需要提高頻譜的分辨率,頻譜的分辨率等于處理信號的時間長度的倒數。