
脈沖信號的上升時間是指脈沖瞬時值最初到達規定下限和規定上限的兩瞬時之間的間隔,除另有規定外,下限和上限分別定義為脈沖峰值幅度的10%和90%。在控制領域中,上升時間是指響應曲線從零時刻到首次達到穩態值的時間,通常定義為響應曲線從穩態值的10%上升到穩態值的90%所需的時間。
很多信號完整性問題都是由信號上升時間短引起的,那么信號上升時間和信號帶寬有什么關系呢?
對于數字電路,輸出的通常是方波信號,方波的上升邊沿非常陡峭,根據傅里葉分析,任何信號都可以分解成一系列不同頻率的正弦信號,方波中包含了非常豐富的頻譜成分。
拋開枯燥的理論分析,我們用實驗來直觀的分析方波中的頻率成分,看看不同頻率的正弦信號是如何疊加成為方波的。
首先我們把一個1.65V的直流和一個100MHz的正弦波形疊加,得到一個直流偏置為1.65V的單頻正弦波。我們給這一信號疊加整數倍頻率的正弦信號,也就是通常所說的諧波。
3次諧波的頻率為300MHz,5次諧波的頻率為500MHz,以此類推,高次諧波都是100MHz的整數倍。
圖1是疊加不同諧波前后的比較,左上角的是直流偏置的100MHz基頻波形,右上角是基頻疊加了3次諧波后的波形,有點類似方波了,左下角是基頻+3次諧波+5次諧波的波形,右下角是基頻+3次諧波+5次諧波+7次諧波的波形。這里可以直觀的看到疊加的諧波成分越多,波形就越像方波。
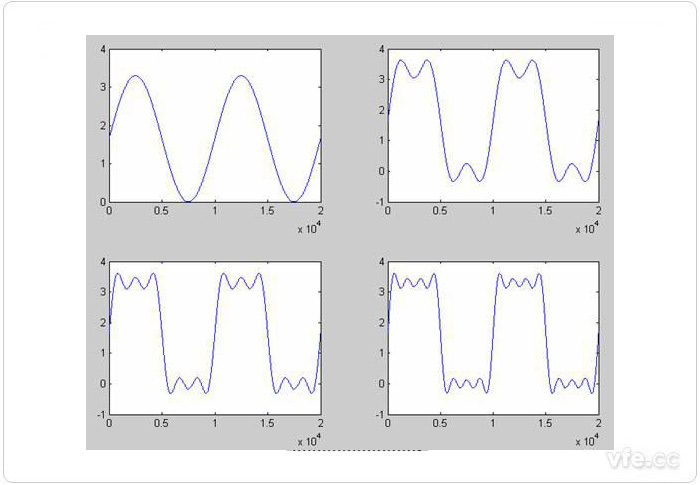
圖1 疊加不同諧波前后比較
因此如果疊加足夠多的諧波,我們就可以近似的合成方波,圖2是疊加到217次諧波后的波形,已經非常近似方波了,不用關心角上的那些毛刺,那是著名的吉伯斯現象,不影響對問題的理解。
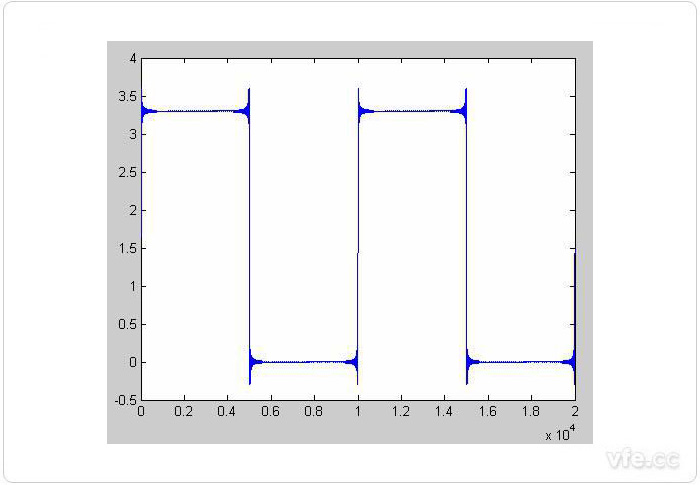
圖2 疊加217次諧波后的波形
上面的實驗非常有助于我們理解方波波形的本質特征,理想的方波信號包含了無窮多的諧波分量,可以說帶寬是無限的。實際中的方波信號與理想方波信號有差距,但是有一點是共同的,就是所包含頻率很高的頻譜成分。
現在我們看看疊加不同頻譜成分對上升沿的影響。圖3是對比顯示,藍色是基頻信號上升邊沿,綠色是疊加了3次諧波后的波形的上升邊沿,紅色是基頻+3次諧波+5次諧波+7次諧波后的上升邊沿,黑色是一直疊加到217次諧波后的波形上升邊沿。
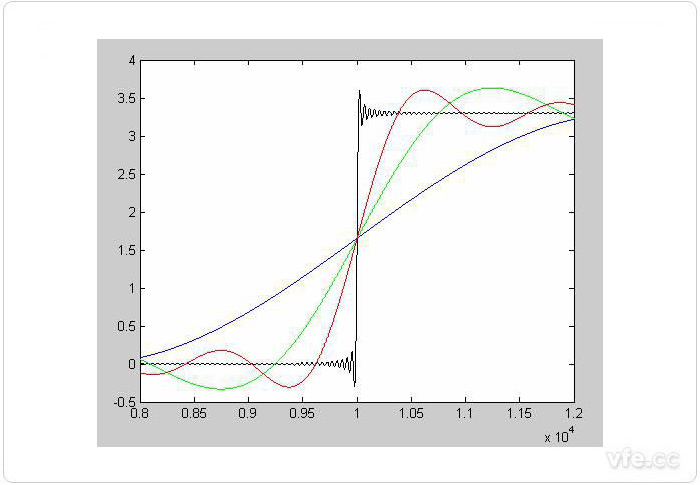
圖3 疊加不同諧波后的波形上升邊沿比較
通過圖3我們可以看到,諧波分量越多,上升沿越陡峭。或從另一個角度說,如果信號的上升邊沿很陡峭,上升時間很短,那該信號的帶寬就很寬。上升時間越短,信號的帶寬越寬。
這里說一下,最終合成的方波,其波形重復頻率就是100MHz。疊加諧波只是改變了信號上升時間。信號上升時間和100MHz這個頻率無關,換成50MHz也是同樣的規律。如果你的電路板輸出數據信號只是幾十MHz,你可能會不在意信號完整性問題。但這時你想想信號由于上升時間很短,頻譜中的那些高頻諧波會有什么影響?記住一個重要的結論:影響信號完整性的不是波形的重復頻率,而是信號的上升時間。