實際電網信號不是理想的周期信號，即便是較為嚴格的周期信號，測量前間諧波頻率為未知量。上述原因導致傅里葉時間窗很可能不等于信號的周期(最低頻率間諧波的周期)的整數倍，也就是很可能不是整周期截斷，而非整周期截斷，必然帶來頻譜泄露，頻譜泄漏后，頻譜上將出現虛假的譜線。這種情況下，單根譜線不能反映真實情況。

　　我們將諧波及諧波兩側一組間諧波的方和根值來反映某個頻段的諧波情況，于是，又引入了諧波群的概念。

　　用200mS的傅里葉時間窗，經過傅里葉變換，我們得到如下圖所示的頻譜圖。圖中加粗的譜線的頻率為基波頻率的整數倍，代表各次諧波的幅值;較細的譜線的頻率為基波頻率的分數倍，代表各間諧波的幅值，某些文獻稱低于基波頻率的間諧波為次諧波。如圖所示以n次諧波譜線為中心，左右各4根譜線及第五根譜線的1/2加上n次諧波為n次諧波群。

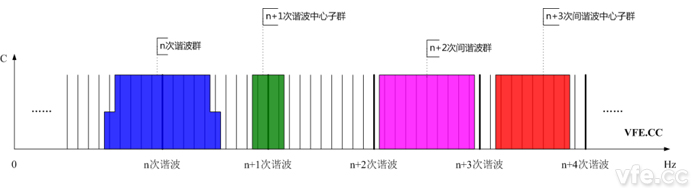
　　圖示：諧波群、間諧波群、諧波中心子群及間諧波中心子群頻譜示意圖

　　諧波群概念的引進是為了方便我們在對某一個頻段的諧波進行評估，而對某一個頻段的諧波進行評估時，人們習慣用頻譜的能量累加來描述。為此，我們定義了諧波群有效值(Gg，n)，諧波群有效值是指某一個諧波有效值以及在時間窗之內靠近它的頻譜分量有效值的方和根，從而，我們就把諧波以及相鄰線譜的能量值累加在一起，從能量的角度來對某一頻段諧波進行衡量。

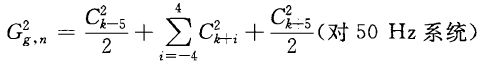
　　……50Hz系統n階諧波群有效值

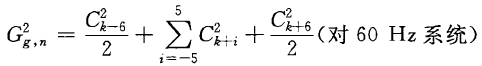
　　……60Hz系統n階諧波群有效值

　　注：

　　對于50Hz系統，傅里葉時間窗取200mS，DFT的頻率分辨率為5Hz，得到頻率間隔為5Hz的系列頻率分量CK+i，K就是頻率分量頻率與基波頻率相除的整數部分，i為余數部分，當i=0時，表示該分量為諧波分量，k為諧波次數，當i≠0時，Ck+i表示k次諧波及k+1次諧波之間的間諧波。(對于50Hz電力系統而言，i的取值在1~9之間，對于60Hz電力系統而言，i的取值在1~11之間)