
自整角機包括:
A、使用于信號傳輸系統作檢測元件用的控制式自整角機;
控制式自整角機包括控制式發送機ZKF和控制式變壓器ZKB。
B、使用于力矩傳輸系統作指示用的力矩式自整角機。
力矩式自整角機包括力矩式發送機ZLF和力矩式接收ZLJ。
控制式自整角機是作為角度和位置的檢測元件,可以將轉角轉換成電信號或將角度的數字量轉變為電壓模擬量,而且精密程度較高,誤差范圍僅有3′~14′。因此,控制式自整角機用于精密的閉環控制的伺服系統中是很適宜的。
力矩式自整角機用做遠距離轉角指示,即將機械角度變換為力矩輸出,但無力矩放大作用,接收誤差稍大,負載能力較差,其靜態誤差范圍為0.5°~2°。因此,力矩式自整角機只適用于輕負載轉矩及精度要求不太高的開環控制的伺服系統里。
自整角機是一種將轉角變換成電壓信號或將電壓信號變換成轉角,以實現角度傳輸、變換和指示的元件。它可以用于測量或控制遠距離設備的角度位置,也可以在隨動系統中用作機械設備之間的角度聯動裝置,以使機械上互不相聯的兩根或兩根以上轉軸保持同步偏轉或旋轉。通常是兩臺或多臺組合使用,產生信號一方的自整角機稱為發送機,接收信號一方的自整角機稱為接收機。
自整角機是一種微型電機,所以自整角機和一般旋轉電機的結構相似,主要由定子和轉子兩大部分組成。下面根據自整角機的使用用途,分別介紹控制式自整角機和力矩式自整角機的工作原理。
控制式自整角機的工作原理可以由圖1來說明。圖1中,由結構、參數均相同的兩臺自整角機構成自整角機組。一臺用來發送轉角信號,稱為自整角發送機,用ZKF表示,它的勵磁繞組接到單相交流電源上。另一臺用來接收轉角信號并將轉角信號轉換成轉子繞組中的感應電動勢輸出,稱之為自整角接收機,用ZKJ表示。兩臺自整角機定子中的整步繞組(定子繞組)均接成星形,三對相序相同的相繞組分別接成回路。

圖1控制式自整角機工作原理圖
在自整角發送機的勵磁繞組中通入單相交流電流時,兩臺自整角機的氣隙中都將產生脈振磁場。脈振磁場使自整角發送機整步繞組的各相繞組生成時間上同相位的感應電動勢,電動勢的大小取決于整步繞組中各相繞組的軸線與勵磁繞組軸線之間的相對位置。當整步繞組中的某一相繞組軸線與勵磁繞組軸線重合時,該相繞組中的感應電動勢為最大值,用E表示電動勢的最大值。
設發送機整步繞組中的A相繞組軸線與其對應的勵磁繞組軸線的夾角為θ1,接收機整步繞組中的A相繞組軸線與其對應的勵磁繞組(轉子繞組)軸線的夾角為θ2,如圖1所示。發送機整步繞組中各相繞組的感應電動勢有效值為:
Ea=E*cosθ1
Eb=E*cos(θ1+120°)
Ec=E*cos(θ1-120°)
由于各相整步繞組對應接成回路,所以感應電動勢在各相繞組中產生感應電流,設Z為ZKF相繞組的阻抗ZF、ZKJ相繞組的阻抗ZJ和連接線的阻抗ZL之和,Z=ZF+ZJ+ZL,I=E/Z(I為勵磁磁通軸線和定子繞組軸線重合時定子某相電流的有效值,每相最大電流有效值),則ZKF與ZKJ的各相繞組回路中產生各相電流為:
Ia=I*cosθ1
Ib=I*cos(θ1+120°)
Ic=I*cos(θ1-120°)
三相對稱整步繞組流過電流時,感應電流產生感應磁場。分析整步繞組電流產生的感應磁場,其合成磁場方向在勵磁繞組的軸線上,且根據楞次定律,合成磁場必定對勵磁磁場起去磁作用,所以合成磁通密度相量B在勵磁繞組軸線上,方向與勵磁繞組產生的磁通密度相量Bj相反。
發送機和接收機的三相定子繞組是對應連接的,所以各對應相的電流大小相等、方向相反,所以接收機合成磁場軸線也與D’1相相夾θ1,但方向與發送機中的合成磁場相反,該磁場以B’表示。
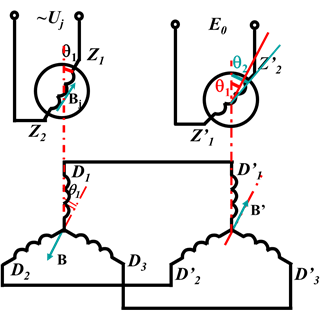
圖2自整角機定、轉子磁場關系
當接收機轉子繞組軸線與定子繞組軸線差θ2時,合成磁場的軸線與接收機轉子繞組軸線夾角為θ2-θ1=d,則合成磁場在接收機轉子繞組中產生的感應電勢的有效值為:
E0=E0max*cosd
E0max是定子合成磁場軸線與轉子繞組軸線重合時的感應電勢,此時達到最大。
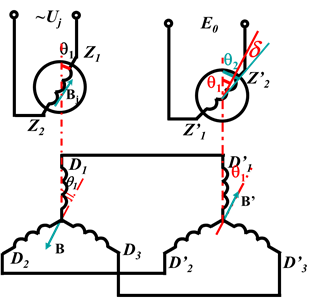
圖3定子合成軸線與輸出繞組軸線夾角
通常把d=90°(與定子B垂直)的位置作為協調位置,偏離此位置的角度叫失調角g,g=90°-g。
E0=E0max*cosg=E0max*sing
由于接收機轉子不轉動,即θ2保持恒定。所以接收機輸出電動勢的大小反映了發送機轉子的偏轉角度,輸出電動勢的極性反映了發送機轉子的偏轉方向,從而實現了將轉角轉換成電信號。
帶電的閉合導體在交變磁場中會產生感生電動勢并產生電流,載流導體在磁場中將受到安培力的作用。因此在控制式自整角接收機的轉子繞組也施加交流激磁電壓時,接收機的轉子就可以帶動一定的負載轉動。力矩式自整角機就是利用這個原理進行工作的(圖4為力矩式自整角機的工作原理圖)。
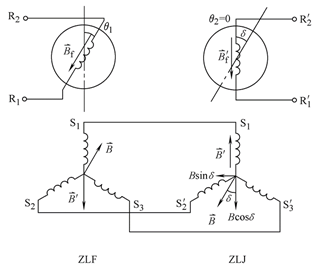
圖4力矩式自整角機原理圖
應用疊加原理分別考慮ZLF勵磁磁通和ZLJ勵磁磁通的作用,所以ZLF和ZLJ同時勵磁定子繞組所產生的合成磁場應該是B和B‘的疊加。
為分析方便將ZLJ中的B分解成兩個分量,直軸分量B*(1-cosd)與轉子電流if相互作用產生電磁力,但不產生轉矩。交軸分量B*cosd與if相互作用產生轉矩。
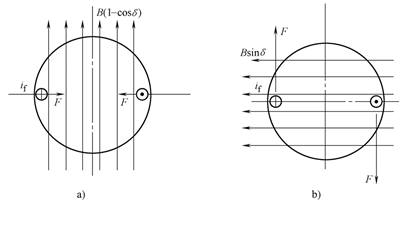
圖6轉子電流與定子磁場相互作用產生轉矩
在該轉矩作用下使失調角d減小,當其為零后B*sind=0,轉矩為零,使ZLJ轉子軸線停止在與ZLF轉子軸線一致的位置上;當d=90°時,產生最大整步轉矩,最大整步轉矩用Tm表示,那么接收機的整步轉矩可以表示為
T=Tm*sind
(1)電氣誤差Δre
自整角發送機定子繞組中的感應電勢理論值滿足:
E1 = E cosq1 E2 = Ecos (q1 +120°) E3 = E cos (q1 -120°)
但由于設計、工藝、材料等因素的影響,各組線電勢的實際值不等于理論值。轉動轉子使其偏離給定的電氣角,直到實際的線電勢和理論值相等。將電氣角和實測角相比,超前為正誤差,滯后為負誤差。每隔15°測一次。正、負最大誤差絕對值之和的一半定義為發送機的電氣誤差,Δdm為最大誤差。
Δre=(|+Δdm|+|-Δdm|)/2
(2)零點位電壓U0
接收機轉子與發送機轉子處于協調位置時輸出繞組出現的端電壓叫零位電壓或殘余電壓。一般有50~180 mV的殘余電壓。
(3)比電壓Uθ
ZKJ在協調位置附近單位失調角(取 g=1°)時的輸出電壓稱為比電壓Uθ,比電壓大同樣大小的失調角所獲得的信號電壓也大,因此系統的靈敏度高 。
(4)輸出相位移Φ
輸出相位移是指ZKJ輸出電壓的基波分量對ZKF勵磁電壓基波分量的時間相位差。目前,國產ZKJ的輸出相位移為2°~20°。
(5)速度誤差Δrv
當轉子轉速較高時,由于發送機定子繞組切割轉子磁場產生切割電勢,并在兩定子繞組中產生附加電流和磁場,因而在ZKJ輸出繞組中感應電勢,稱為速度電勢。由于速度電勢的存在,使得ZKJ轉子最后所處的位置不是g=0的地方,而是偏離協調位置Δrv。這樣,就造成了速度誤差Δrv。轉速越高,速度電勢越大,速度誤差也越大。
(1)阻尼時間td
指強迫接收機轉子失調(177±2)°,放松后,經過衰減振蕩達到協調位置時所需要的時間。按規定阻尼時間不應大于3s。阻尼時間越短,表示接收機的跟隨性能越好。為此,在力矩式接收機中通常都裝有阻尼繞組,也有的裝有機械阻尼器。
(2)零位誤差Δθ0
當ZLF的轉子勵磁后,在理論上,從線電動勢為零的某一位置(基準零位)開始,轉子每轉過60°,整步繞組中必有一線電動勢(Eab或Ebc或Eca)為零,此位置稱為理論電氣零位。 但是由于設計、工藝、材料等因素的影響,實際電氣零位與理論電氣零位存在著差異,兩者之差稱為力矩式自整角機的零位誤差。
(3)比整步轉矩Tθ
指力矩式自整角發送機和接收機在協調位置附近失調角為1°時所產生的整步轉矩。即
Tθ=Tm*sin1°
比整步轉矩越大,其整步能力越強,靜態誤差越小,所以比整步轉矩是ZLJ的一項重要性能指標。一般產品數據中均列出它的數值。
(4)靜態誤差 Δθs
發送機處于停轉或轉速很低時的工作狀態稱為靜態。在理想情況下,接收機應與發送機轉過相同的角度。但由于接收機軸上存在摩擦轉矩和阻尼轉矩,所以使兩機的轉角出現差值。把靜態空載運行而達到協調位置時,發送機轉子轉過的角度與接收機轉子轉過的角度之差稱為靜態誤差。
靜態誤差通常用度或角分表示,它決定接收機的精度。根據靜態誤差的大小可分為三個精度等級:0級為0.5°,1級為1.2°,2級為2°。
圖7是雷達俯仰角自動顯示系統示意圖。圖中自整角發送機2轉軸直接與雷達天線的俯仰角α耦合,因此雷達天線的俯仰角α就是自整角發送機的轉角。控制式自整角接收機1轉軸與由交流伺服電動機3驅動的系統負載(刻度盤5或火炮等負載)的軸相連,其轉角用β表示。接收機轉子繞組輸出電動勢E2(有效值)與兩軸的差角γ即α-β近似成正比,即
E2=K(α-β)=K*γ…………時鐘K為常數
E2經放大器放大后送至交流伺服電動機的控制繞組,使交流伺服電動機轉動。可見,只要α≠β,即γ≠0,就有E2≠0,伺服電動機便要轉動,使γ減小,直至γ=0。如果α不斷變化,系統就會使β跟著aα變化,以保持γ=0,這樣就達到了轉角自動跟蹤的目的。只要系統的功率足夠大,接收機上便可帶動火炮一類阻力矩很大的負載。發送機和接收機之間只需三根連線,便實現了遠距離顯示和操縱。

圖7雷達俯仰角自動顯示系統原理圖
1—自整角接收機;2—自整角發送機;3—交流伺服電動機;4—放大器;5—刻度盤;6—減速器
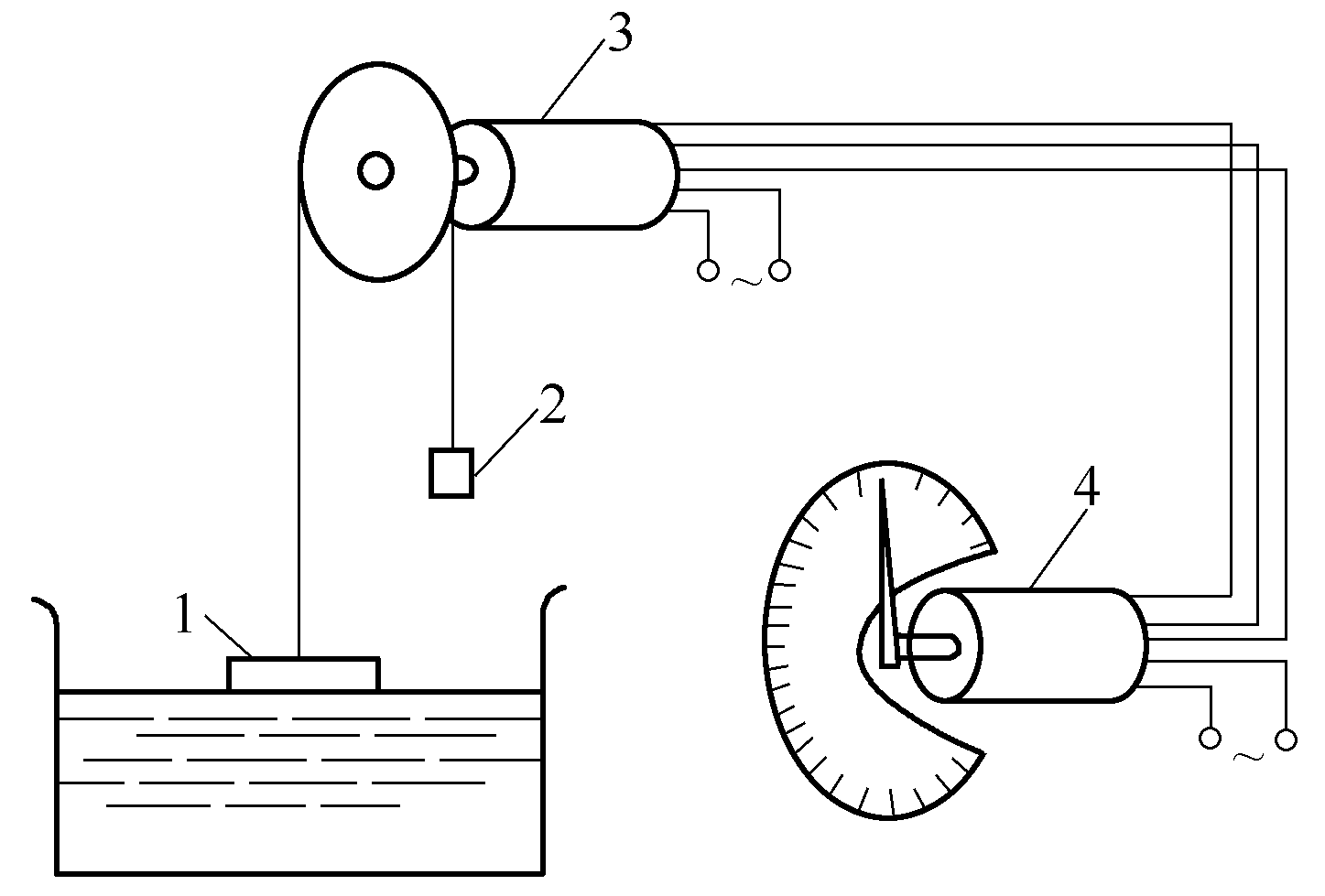
圖8液面位置指示器
1—浮子;2—平衡錘;3—發送機;4—接收機
圖9為自整角機電氣參數測試原理圖。自整角機的測試包括勵磁繞組及整步繞組的電壓、電流、頻率、功率、諧波及相關相位角等參數。同時,通過相關上位機軟件運算,還可計算出電氣誤差、零位電壓、比電壓、輸出相位移、速度誤差、零位誤差、靜態誤差等參數。

圖9自整角機電氣參數測試原理圖